K-Nearest Neighbors (KNN) is a simple yet powerful supervised learning algorithm used primarily for classification tasks, although it can also be adapted for regression. It’s a non-parametric and lazy learning algorithm, meaning it doesn’t make any assumptions about the underlying data distribution and doesn’t learn an explicit model during training. Instead, it stores the entire training dataset in memory and uses it to make predictions on new, unseen data points.

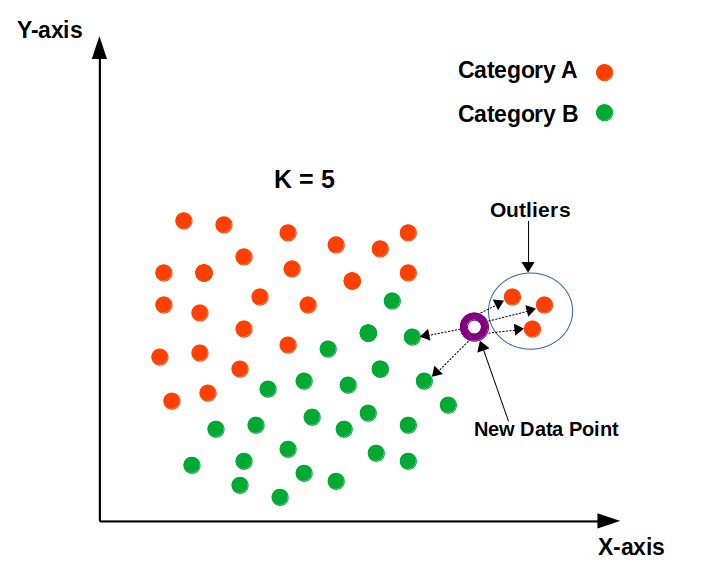
How K-NN Works:

Training Phase:

• Data Storage: The KNN algorithm essentially “memorizes” the entire training dataset. No explicit model is built during this phase.

Prediction Phase:

• Distance Calculation: When presented with a new, unseen data point, the algorithm calculates the distance between this point and all the data points in the training set.
  • Common Distance Metrics:
    • Euclidean Distance: The most commonly used distance metric, calculated as the square root of the sum of squared differences between corresponding features.
      • Formula: √(∑(x1i – x2i)²) where x1i and x2i are the values of the ith feature for the two data points.
    • Manhattan Distance: Calculated as the sum of absolute differences between corresponding features.
      • Formula: ∑|x1i – x2i|
• K-Nearest Neighbors: The algorithm identifies the ‘k’ nearest neighbors to the new data point based on the calculated distances. The value of ‘k’ is a crucial hyperparameter that needs to be carefully chosen.  
• Classification:
  • In classification tasks, KNN assigns the new data point to the class that is most frequent among its ‘k’ nearest neighbors. This is often referred to as “majority voting.”
• Regression:
  • In regression tasks, KNN predicts the value for the new data point by averaging (or taking a weighted average) of the target values of its ‘k’ nearest neighbors.

Choosing the Right k Value

The choice of the parameter ‘k’ significantly impacts the performance of the KNN algorithm:

• Small k:
  • Can be sensitive to noise and outliers in the data.
  • May lead to overfitting, where the model performs well on the training data but poorly on unseen data.
• Large k:
  • Can smooth out noise and improve generalization, but may miss local patterns in the data.
  • May lead to underfitting, where the model fails to capture the underlying patterns in the data.

Finding the optimal value of ‘k’ often requires experimentation and techniques like cross-validation.

Advantages of KNN:

• Simplicity: Easy to understand and implement.
• Versatility: Can be used for both classification and regression.
• No Training Phase: Requires minimal training time.
• Effective for Complex Decision Boundaries: Can capture complex non-linear relationships in the data.

Disadvantages of KNN:

• Sensitive to the choice of ‘k’.
• Computational Cost: Can be computationally expensive for large datasets, especially during the prediction phase, as it requires calculating distances to all training points.  
• Sensitive to noisy data and outliers.
• Curse of Dimensionality: Performance can degrade significantly in high-dimensional spaces.

Applications of KNN:

• Recommendation Systems: Recommending products, movies, or music based on user preferences and the preferences of similar users.
• Image Recognition: Classifying images based on visual features.
• Anomaly Detection: Identifying unusual or abnormal data points.
• Financial Applications: Credit scoring, fraud detection.

KNN Algorithm Example:

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load the iris dataset
iris = load_iris()
X = iris.data
y = iris.target

# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create a KNN classifier with k=3
knn = KNeighborsClassifier(n_neighbors=3) 

# Train the model (Note: KNN has no explicit training phase)
knn.fit(X_train, y_train)

# Make predictions
y_pred = knn.predict(X_test)

# Evaluate accuracy
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

K-Nearest Neighbors is a simple yet effective algorithm with various applications in machine learning. By understanding its strengths and limitations and carefully choosing the value of ‘k’, you can effectively apply KNN to a wide range of classification and regression problems.