Support Vector Machines (SVM) are a powerful supervised machine learning algorithm used for both classification and regression tasks. SVMs are known for their ability to find the optimal decision boundary that maximizes the margin between different classes, leading to robust and effective models.

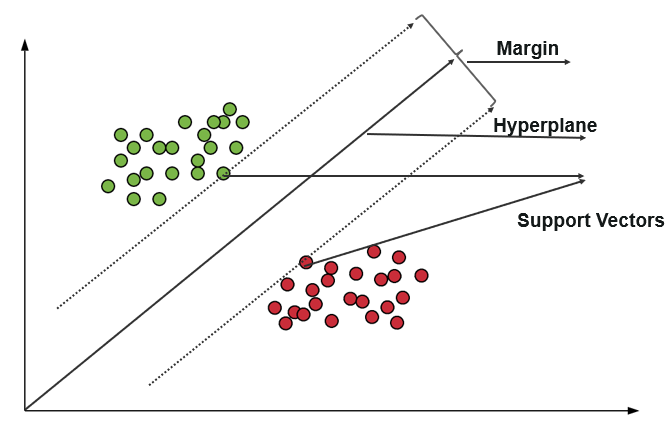
Key Concepts:

• Hyperplane: In SVM, the decision boundary is represented by a hyperplane. In two dimensions, this is a line; in higher dimensions, it’s a plane or a more complex surface.
• Support Vectors: These are the data points that lie closest to the hyperplane. The position and orientation of the hyperplane are entirely determined by these support vectors.
• Margin: The distance between the hyperplane and the nearest data points (support vectors) from each class. The goal of SVM is to find the hyperplane that maximizes this margin.

Types of SVM:

1. Linear SVM

• Used when the data is linearly separable.
• Finds the optimal hyperplane that separates the data into two classes with the largest possible margin.

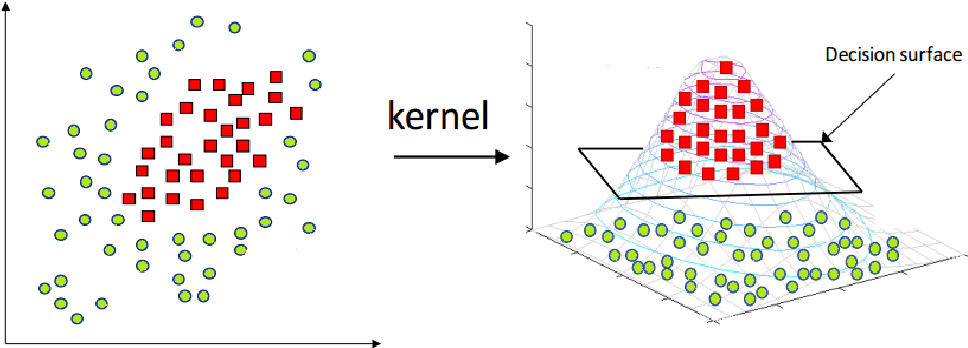
2. Non-Linear SVM (using Kernel Trick)

• Used when the data is not linearly separable.
• The kernel trick maps the data into a higher-dimensional space where it becomes linearly separable.

SVM for Binary Classification in Python

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC 
from sklearn.metrics import accuracy_score

# Load the iris dataset
iris = load_iris()

# Select two features and two classes
X = iris.data[:100, [1, 2]]  # Sepal Width and Petal Length
y = iris.target[:100] 

# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create an SVM classifier with an RBF kernel
svm_classifier = SVC(kernel='rbf', C=1.0, gamma='scale') 

# Train the model
svm_classifier.fit(X_train, y_train)

# Make predictions on the test set
y_pred = svm_classifier.predict(X_test)

# Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

Common kernels include:

Radial Basis Function (RBF) Kernel: Maps data to an infinite-dimensional space.
Polynomial Kernel: Maps data to a polynomial space.

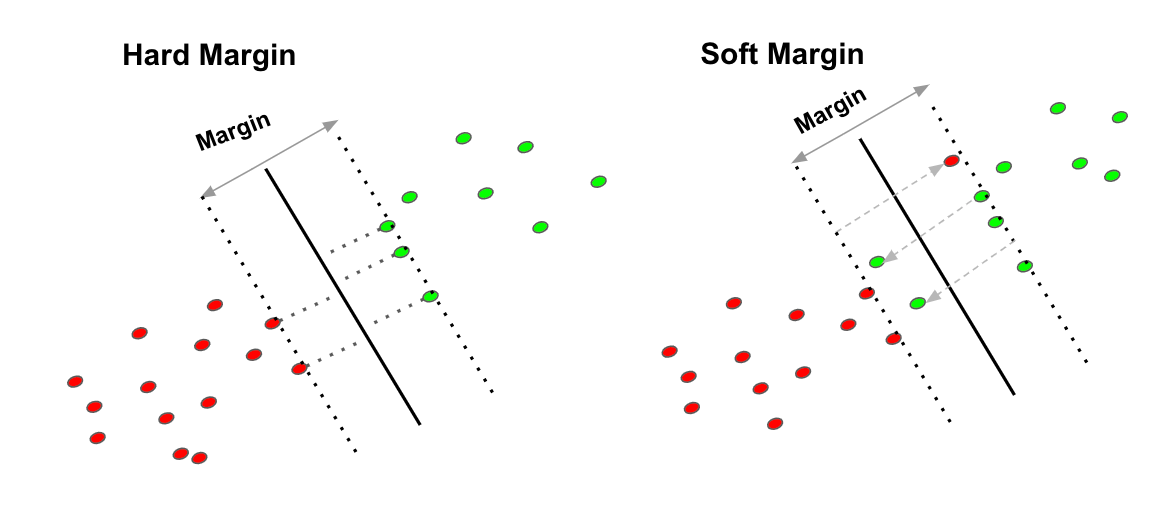
Hard Margin SVM:

Assumption: Assumes that the data is perfectly linearly separable.

Goal: Find the hyperplane that perfectly separates the data without any misclassifications.

Limitations:

• Can be sensitive to outliers and noise in the data.
• May not be suitable for real-world datasets that often contain some degree of noise or overlap between classes.

Soft Margin SVM:

More realistic: Allows for some misclassification to handle noisy or overlapping data.

Introduces a penalty: Introduces a penalty term in the optimization objective to allow for a small number of misclassifications.

Regularization Parameter (C): Controls the trade-off between maximizing the margin and minimizing the number of misclassifications.

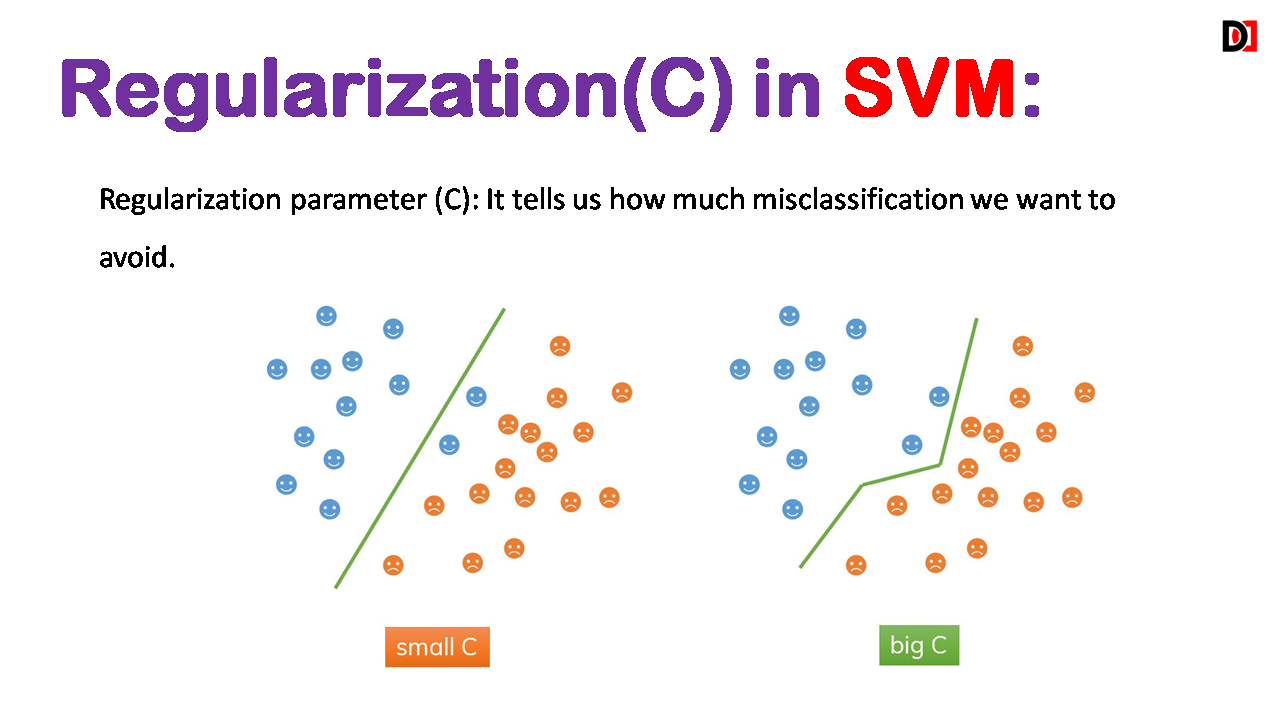
• High C: Prioritizes minimizing misclassifications, potentially leading to overfitting.
• Low C: Prioritizes maximizing the margin, potentially leading to underfitting.

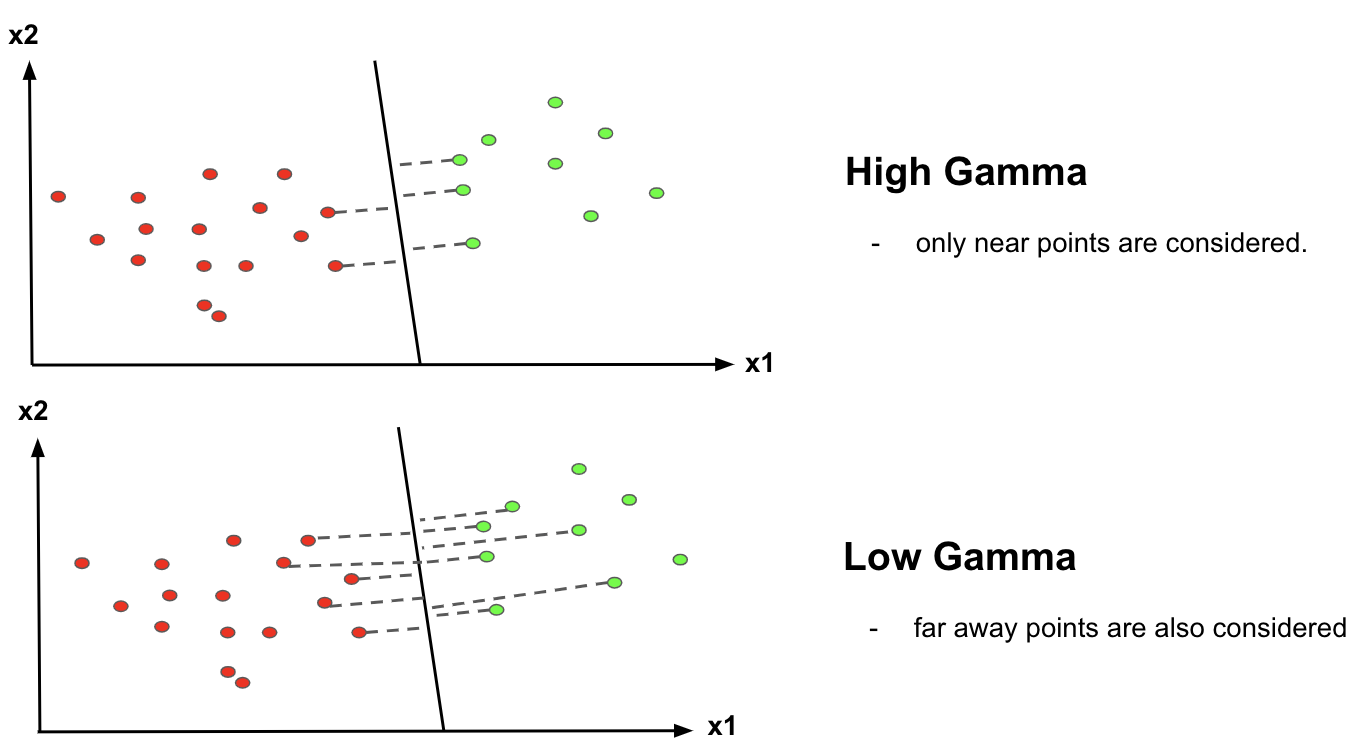
Gamma Parameter (in RBF Kernel)

Influence of data points: The gamma parameter in the RBF kernel controls the influence of individual data points on the decision boundary.

• High gamma: Gives more weight to data points close to the decision boundary, leading to a more complex decision boundary.
• Low gamma: Gives more weight to data points farther from the decision boundary, leading to a smoother decision boundary.

Key Advantages of SVM:

• Effective in high-dimensional spaces.
• Robust to overfitting (with appropriate parameter tuning).
• Versatile with the use of different kernels.
• Can handle both linear and non-linear data.

Limitations:

• Can be computationally expensive for large datasets.
• Choosing the optimal kernel and hyperparameters can be challenging.
• Less interpretable compared to some other models.

Support Vector Machines are a powerful and versatile machine learning algorithm with a strong theoretical foundation. By understanding the key concepts and techniques, you can effectively apply SVM to a wide range of classification and regression problems.